Comment fonctionne un réseau de neurones, pour les nuls

Avec le moins de jargon possible!

La plupart des explications sur le fonctionnement d’un réseau de neurones sont simplistes ou excessivement mathématiques. Je vais essayer d’éviter ces deux écueils.

La métaphore du patron

Imaginons le chef d’un fonds d’investissement cherchant à faire prédire à ses employés les performances d’une entreprise après qu’ils aient lu leur dernier rapport financier.

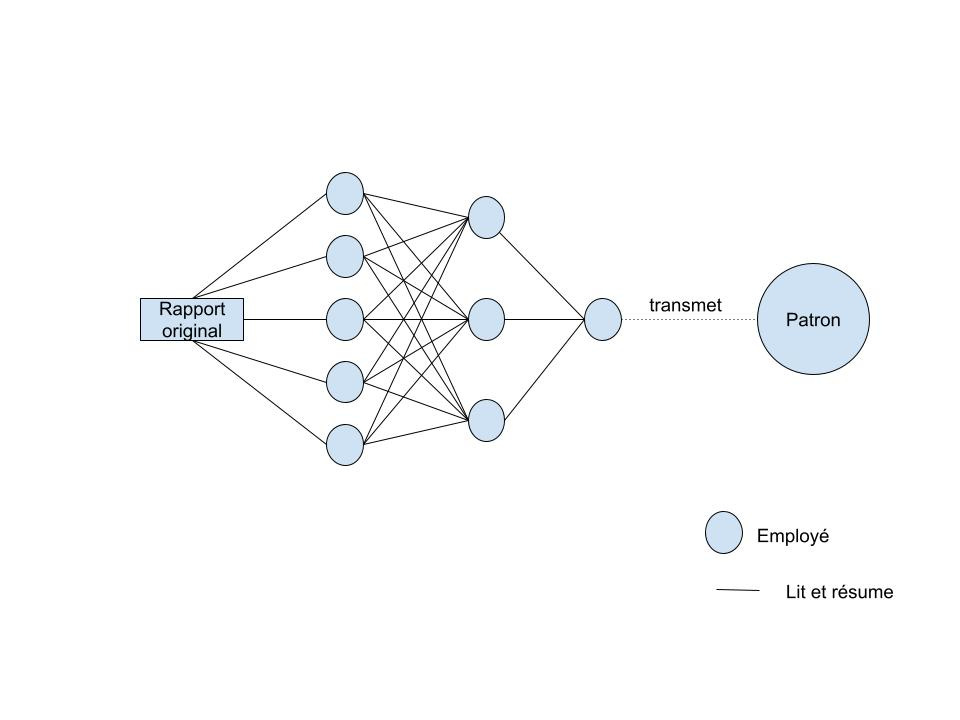
Il demande à 5 d’entre eux de lire leur rapport financier, de le résumer et de donner leur opinion personnelle sur le sujet. Il demande à 3 autres employés de lire les 5 résumés faits par les premiers, de faire leur propre résumé et de donner leur sentiment. Enfin, un dernier employé rassemble les opinions de ces 3 là, fait son propre résumé, donne son propre sentiment et le transmet au patron.

Le patron, lui, est omniscient, et sait ce qu’un résumé parfait est censé contenir, et sait quel sentiment on doit ressentir à la lecture du rapport. Alors une fois le rapport final obtenu, il dit à son employé le plus proche (le dernier de la liste): Tu devrais être plus optimiste/pessimiste dans ton analyse: tu es biaisé. Aussi, tu fais bien d’accorder beaucoup de poids à ce que dit l’employé n°3 de la deuxième couche, c’est lui qui est le plus proche de la réalité. Accorde-s-en encore plus. Il dit ensuite aux employés de la deuxième couche: n°3, tu es celui que mon employé favori écoute le plus, alors je tiens à ce que tu saches que tu es un peu biaisé, et que tu devrais accorder plus de poids à ce que dit l’employé n°4 de la troisième couche. n°2, tu ne sers pas à grand chose: change ton biais plutôt comme ça et tes poids plutôt dans ce sens là, mais ne te force pas trop, tu es inutile. N°1, idem. Il s’adresse ensuite aux employés de la troisième couche, en leur tenant un discours similaire.

Ce qu’il faut comprendre, c’est qu’en connaissant le comportement des employés de la couche n (le fameux employé de la première couche qui écoute beaucoup le n°3 de la deuxième couche), le patron peut dicter aux employés de la couche n+1 le comportement à adopter pour diminuer l’erreur finale. Comme c’est récurrent, le patron sait exactement quoi dire à ses 9 employés.

Et à chaque lot de {batch_size} rapports lus, le patron fait des retours comme cela à ses employés. Au bout d’un moment, le dernier employé lui dira exactement ce qu’il veut entendre.

Cet apprentissage par “retours récursifs” est à la base de l’entraînement des réseaux de neurones. On l’appelle plus communément BackPropagation.

<pour les matheux>

Passer de la métaphore à la réalité est assez simple:

• À la place des employés, on a des neurones, qui prennent en entrée les résultats des couches précédents, et qui renvoient un nombre, calculé à partir de ces entrées et d’une fonction d’activation. Une fonction d’activation typique est la fonction Relu. La fonction d’activation est immuable, mais le poids accordé à chacune des entrées est variable et entraînable, on va voir comment. Aussi, la sortie du neurone peut être offsetté d’un certain nombre, appelé biais. Idem, ce biais est entraînable.

• À la place d’un patron, on a une fonction d’erreur qui prend en paramètre 1) l’output du réseau de neurone et 2) la réalité, et qui sort un nombre, appelé erreur.

• Connaissant l’architecture du réseau de neurones et les fonctions d’activation de chacun des neurones, il est possible d’évaluer la dérivée partielle de l’erreur par rapport à chacun des biais et des poids des neurones. L’entraînement consiste, plus ou moins par la méthode de Newton (stochastic gradient descent), à minimiser cette erreur en les faisant varier.

• Théoriquement, on pourrait utiliser cette approche avec n’importe quel type de fonction. Imaginons que l’on prenne un polynôme de degré 5 à deux variables il aura donc 10 termes, et 10 coefficients. Si on cherche à approximer par ce polynôme une fonction arbitraire à 2 paramètres, on pourra calculer la dérivée partielle de l’écart entre l’approximation et la réalité par rapport aux différents coefficients de notre polynôme. Et en connaissant cette dérivée partielle, on pourra, toujours par stochastic gradient descent, trouver les coefficients optimaux de notre polynôme.

• Cependant, les réseaux de neurones ont un avantage architectural très important sur ces polynômes: leur structure “en couche“ permet d’utiliser la chain rule, qui limite la complexité des calculs de dérivées partielles. On peut utiliser les dérivées partielles de la couche n pour calculer ceux de la couche n+1. Ça donne aux réseaux de neurone un rapport “niveau de non-linéarité modélisable / complexité de calcul des dérivées partielles” très avantageux.

</pour les matheux>

Un cas pratique: évaluer le PH d’une solution à partir de la photo d’une bandelette

La photo d’une bandelette trempée dans une solution à PH 13.

Notre réseau de neurones prend donc en entrée la photo (ou plutôt la valeur de vert, bleu et rouge de chaque pixel) de la bandelette, et doit renvoyer un nombre réel (pas forcément entier, donc) entre 0 et 14. Le réseau doit être performant malgré la diversité de prises de vues (plus ou moins zoomées, plus ou moins lumineuses, etc…)

Avant l’ère du machine learning, l’approche aurait été d’appliquer des filtres très restrictifs sur l’image. Par exemple, sur l’image d’en haut, des filtres de différentes teintes de violet ne laissant passer qu’une bande restreinte de couleurs.

Il aurait fallu ensuite compter le nombre de pixels ainsi “autorisés” par chaque filtre, puis construire un modèle complexe liant le nombre de pixels “autorisés” par chacun d’entre eux à un résultat de PH.

Donc:

1. Appliquer des filtres

2. Créer un modèle liant le résultat des filtres à un chiffre de PH

L’approche machine-learning (ML) de ce problème est très similaire. La grande avancée est que:

1. Les filtres sont entraînables

2. Le modèle aussi

Ainsi, pour ce genre de tâches, on utilise des réseaux de neurones convolutionnels (CNN ou Convnet en anglais). Ils sont dits convolutionnels parce qu’ils appliquent des filtres sur une image, à travers une opération dite de convolution. Étant donné que ce post n’est pas destiné à un public matheux (c’est là une immense frustration), ceux qui sont à l’aise dans le domaine pourront lire cet article, expliquant très bien le fonctionnement d’un Convnet. 

J’aimerais juste que le lecteur puisse avoir l’intuition de la façon dont des “filtres” peuvent être entraînés. C’est une chose assez abstraite, du moins en surface.

On peut avoir une bonne intuition de l’algorithme d’entraînement d’un modèle simple, grâce à la métaphore du patron, dans l’article précédent. Mais entraîner des filtres? Comment faire?

Imaginons un filtre simple, qui ne laisse passer qu’une certaine bande de couleur. Par exemple, le filtre ne laisse passer qu’une bande allant du rose au violet. Cela correspond à une certaine valeur acceptable de rouge, vert et bleu (puisque les pixels d’une image ne sont encodés que sur ces trois couleurs primaires). 

Notre filtre nous dit au cours de l’entraînement “Il y a 232 pixels sur notre image qui passent notre filtre”. Le modèle filtre => PH le traduit en “Cela veut dire que le PH affiché par la bandelette est de 8”. On compare ce résultat au résultat attendu, qui est, disons, 13.

Les poids du modèle filtre => PH sont mis à jour à la façon énoncée dans la métaphore du patron, parce que ce modèle a une structure très similaire à celui énoncé dans cette métaphore.

Voyons voir pour le filtre:

L’algorithme de back propagation lui tient à peu près ce langage “Tu m’as dit qu’il y avait 232 pixels ok pour la dernière image. On en a déduit que le PH devait être de 8. Sauf qu’en réalité, le PH est de 13. Pour qu’on soit raccords, il faudrait que le nombre de pixels OK sur la dernière image soit de 422 plutôt que 232. Là, on déduirait le bon PH.”

Il lui dit ensuite “Pour que l’on ait 422 pixels OK, il faudrait que tu sois beaucoup plus permissif sur le bleu, et moins sur le rouge. Change tes poids dans cette direction.”

La prochaine fois qu’on lui présentera l’image du haut (ou une similaire), plus de pixels seront “OK” selon le filtre: il aura “appris” de ses erreurs.

<pour les matheux>

Ceci est une redite, en des termes différents de la section <pour les matheux/> précédente.

L’idée est que, vu qu’on connaît la structure du réseau et son ensemble de paramètres (les fameux poids et biais, qui, dans le cas d’un filtre, correspondent à peu près aux niveaux acceptables des différentes couleurs), on connaît la fonction de transfert entre l’image et le résultat sous forme de PH. On connaît donc la dérivée partielle de l’erreur par rapport à chacun des paramètres du réseau, et on peut donc orienter l’évolution de chacun d’entre eux pour diminuer l’erreur finale. La structure “profonde” d’un réseau permet d’exploiter la chain rule, ce qui rend le calcul des dérivées partielles peu coûteux.

</pour les matheux>

Bref, on voit ici comment on peut entraîner un filtre. En pratique, la chose est très simple: des librairies python permettent de le faire sans se poser de questions. On peut multiplier les filtres, appliquer des filtres sur des images déjà filtrées, ajouter des couches au modèle filtres => PH en quelques lignes de code, et l’optimisation du réseau se fera tout seul à partir des images d’entraînement. Vivent PyTorch et TensorFlow. 

Cependant et comme dirait Andrej Karpathy (ancien directeur IA chez Tesla), il est nécessaire de comprendre comment fonctionne vraiment la back propagation pour ne pas faire d’erreurs bêtes lors du design d’un réseau de neurones. 

Assez peu de data-scientists ou d’ingénieurs IA savent vraiment ce qui se passe sous le capot, ce qui est un peu dommage et qui peut poser pas mal de problèmes.